Factoring integers with sublinear resources on a superconducting quantum processor
So, after my son-in-law sends me the article link, I decided to dig into it a bit more. The story is that a Chinese company published a paper (see it here) claiming to crack RSA code by using only 10 qubits and a Novel math trick. With some math tricks and only 10 noisy qubits, they (China) claim to have paved the way for factoring large integers that have cryptographic significance. So, the Chinees RSA code break is the topic of today's post. The answer is that they only claimed and no proof provided.
My lame math understanding and after reading the published paper suggest they used Shor's math trick and this new method in an innovative way called "lattice reduction." Although the Shor's math trick could threaten global financial security one day, that day may be far in the future. Or is it? Someday, sooner or later, Shor's algorithm will seriously challenge cryptosystems based on public keys, but for this to work in real time, you need a "flawless" quantum machine and another flawless classical supercomputer and flawless math trick. Most people in this business agree we don't have an error-free quantum computer, even if you can break it with clever math tricks. The latest estimates backed by leading mathematicians say that to crack RSA-2048, we would need "millions" of flawless physical and logical qubits, running error-free in real-time, and this is far beyond current technology. But, is it?
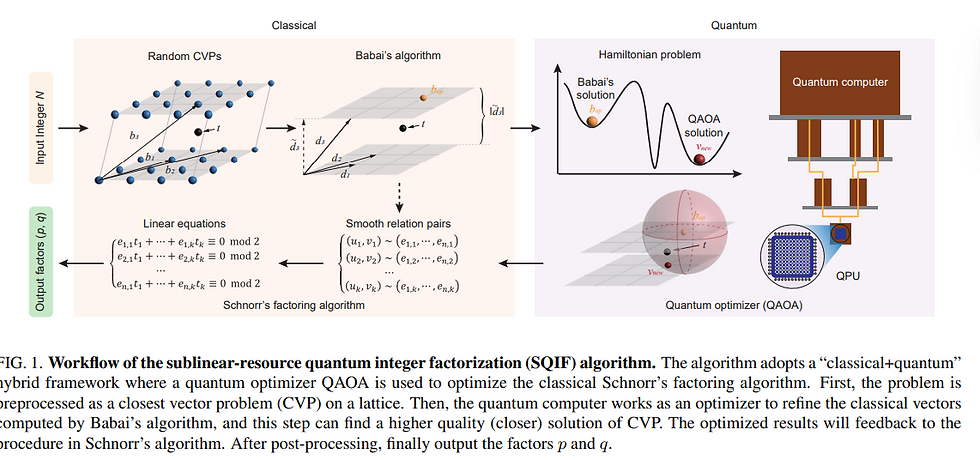
I argue that they (Chinees) should not be taken lightly, however. In both classical and quantum computer development, China has a strong competitive edge. Apparently, they developed a universal quantum algorithm for integer factorization by combining classical "lattice reduction" with a quantum approximate optimization algorithm (QAOA). In that paper, they reveal that this algorithm is the most qubit-saving factorization algorithm to date because it saves O(logN/loglogN), which is sublinear in bit length. That is where I got lost and didn't know what that meant. They claim it is designed around current NISQ quantum devices.

So, i started digging more into this. In other words, the group "demonstrated" the algorithm by factoring 48-bit integers using only 10 superconducting qubits. Well, that's not RSA-2048. Perhaps, they claim that the RSA-2048 can be challenged by this method, but can it be beaten? It's hard to say.
Here is the gist of what they claim based on the paper:
"RSA-2048 can be challenged with our algorithm if you have a quantum circuit with 372 qubits and a depth of thousands. In this study, we "show" that noisy quantum computers can be used more effectively, and we "pave the way" for factoring large integers that have cryptographic significance. "
As a final note:
We don't have any peer-reviewed evidence of how this experiment was conducted. However ,there may be something there that we don't know. What if they built this updated algorithm based on this paper published by Claus P. Schnorr, a German math scientist and crypto expert? And how come it is not classified information if they broke RSA-2048?
I don't get all this math stuff right now, but I'm determined to follow this story.
The 5th of January, 2023

"Paper 2021/933
Fast Factoring Integers by SVP Algorithms, corrected"
https://eprint.iacr.org/2021/933

Comments