The spins:

ERNST ISING ( 1900 - 1998 )
German physicist, who is best remembered for the development of the Ising model. In this blog some of the post defining Ion Trapping content in many cases include the Ising Model and its essential understanding of the model in both classical and quantum physics.
The Ising model, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states.
The Ising model is defined on a discrete collection of variables called spins, which can take on the value 1 or −1.
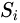
The spins interact in pairs, with energy that has one value when the two spins are the same, and a second value when the two spins are different.
The energy of the Ising model is defined to be:
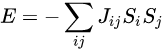
where the sum counts each pair of spins only once. Notice that the product of spins is either +1 if the two spins are the same (aligned), or −1 if they are different (anti-aligned). J is half the difference in energy between the two possibilities. Magnetic interactions seek to align spins relative to one another. Spins become randomized when thermal energy is greater than the strength of the interaction.
For each pair, if

A ferromagnetic interaction tends to align spins, and an antiferromagnetic tends to antialign them.
The spins can be thought of as living on a graph, where each node has exactly one spin, and each edge connects two spins with a nonzero value of J. If all the Js are equal, it is convenient to measure energy in units of J. Then a model is completely specified by the graph and the sign of J.
The antiferromagnetic one-dimensional Ising model has the energy function:
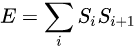
where i runs over all the integers. This links each pair of nearest neighbors.
In his 1924 PhD thesis, Ising solved the model for the 1D case. In one dimension, the solution admits no phase transition. On the basis of this result, he incorrectly concluded that his model does not exhibit phase transition in any dimension.
It was only in 1949 that Ising knew the importance his model attained in scientific literature, 25 years after his Ph.D thesis. Today, each year, about 800 papers are published that use the model to address problems in such diverse fields as neural networks, protein folding, biological membranes and social behavior.
Additional Ising Model learning - short overview
Ising Model simulation on a quantum computer
Abstract
We present an exact simulation of a one-dimensional transverse Ising spin chain with a quantum computer. We construct an efficient quantum circuit that diagonalizes the Ising Hamiltonian and allows to obtain all eigenstates of the model by just preparing the computational basis states. With an explicit example of that circuit for n=4n=4 spins, we compute the expected value of the ground state transverse magnetization, the time evolution simulation and provide a method to also simulate thermal evolution. All circuits are run in IBM and Rigetti quantum devices to test and compare them qualitatively.

Additional reading - Simulation of Quantum Ising Model in an Ion Trap:
This document origin comes from German National Library website.
Or, Download it here


Comments