
Ions trapped using a special version of Paul Trap, named in honor of inventor, Wolfgang Paul. It is the main instrument to trap individual or a group of ions for quantum computation. After we trap, we build gates and then we have the fundamental blocks of quantum computation. Before I jump into the Paul Trap, lets take about Mathieu's equation.

Mathieu’s equation is one of the archetypical equations of nonlinear vibrations theory . However, this equation is not only associated with this field, but due to the tools and techniques needed for its quantitative analysis and diverse applications, it appears also in applied mathematics and in many engineering fields such as Quantum computations. The form of Mathieu’s equation is very simple—it is a linear second-order ordinary differential equation (ODE), which differs from the one corresponding to a simple harmonic oscillator (used for quantum computing) in the existence of a time-varying (periodic) forcing of the stiffness coefficient which is; the ratio of the force acting on a linear mechanical system, such as a spring, to its displacement from equilibrium.
The stiffness coefficient (k) can be calculated using the correlations k = force/displacement. You need all these for ion trapping tracking the Ions' motion (inside the trap) and "pseudo-potential approximation."
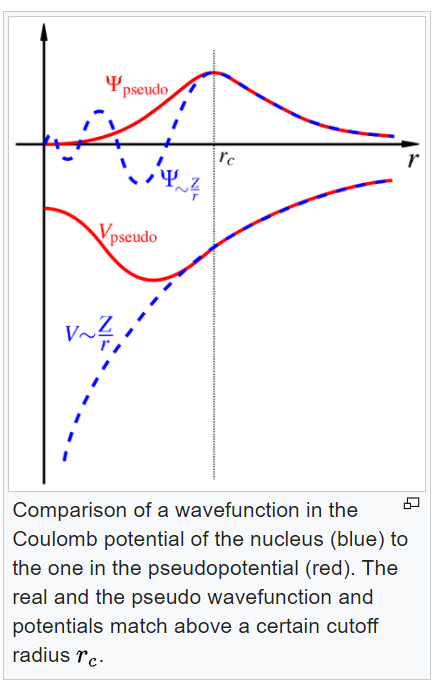
To calculate the classical trajectory of the ion in the paul Trap, we solve the relevant differential equation, the Mathieu equation described above. The motion of ion is approximately calculated based on pseudo-potential, a time-averaged version of the radio frequency (RF) potential that is produced by RF electrodes attached to the Paul Trap. The motion of ion therefore refer to as a superposition of fast oscillation at the RF frequency, which is called micromotion, and the slow orbit called secular motion.

In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering. The pseudopotential approximation was first introduced by Hans Hellmann in 1934.

Back to Ion trapping ions, the trap consists of four metal rods: an RF potential is applied to two of them and the other two are segmented DC electrodes, with each segment held at a different static voltage. The confinement along the y axis - which we refer to as the trap axis - is achieved by setting the static voltages V1 and V2 so as to generate a DC harmonic well along this axis. The total DC potential is:

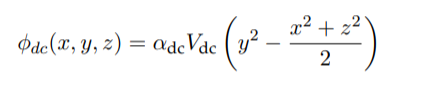
"RF trapping relies on time variation of a potential that, at any instant in time, is anti-confining in at least one dimension. Confinement using this time-variation is enabled due to the inertia of a massive charged particle. It is thus clear that the stability of an ion in such a ponderomotive trapping potential created in this manner would depend on the parameters of both the RF potential, as well as of the ion itself. In fact, the motion of an ion in an RF Paul trap satisfies the Mathieu equation and depends in detail on these parameters, i.e. the ion’s charge-to-mass ratio, the RF frequency, the RF amplitude, and the curvature of the potential. Solutions to the Mathieu equation result in so-called “secular” harmonic bounded motion at a frequency typically somewhat less than half the RF drive frequency. Upon the secular motion is superimposed a higher frequency motion, at the RF drive frequency, known as “micromotion,” and its amplitude is in general time-dependent. The stability of RF Paul traps used for containment of singly-ionized atoms requires the voltage amplitude and frequency of the applied RF to fall in a certain range.
Traps being explored for Quantum Computation have ion-electrode distances in the range of 30 µm to 1 mm, leading to RF voltage amplitudes of 10-1000 V at 10-100 MHz, depending on the exact trap size and atomic species."

Micrometre, also called micron, metric unit of measure for length equal to 0.001 mm, or about 0.000039 inch. Its symbol is μm.
Mathieu’s Equation and Its Generalizations: Overview of Stability Charts and Their Features. Read detailed explanation of this equation from the provided link or down load it here.

Wolfgang Paul
Wolfgang Paul was a German physicist, who co-developed the non-magnetic quadrupole mass filter which laid the foundation for what is now called an ion trap.

Comentarios